Generalized Extreme Value Models for Count Data: Application to Worker Telecommuting Frequency Choices
PI: Rajesh Paleti
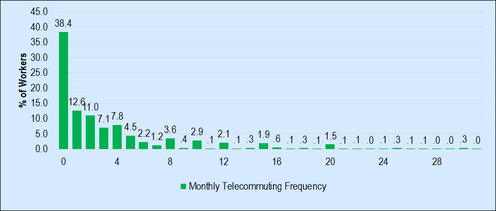
Count models are used for analyzing outcomes that can only take non-negative integer values with or without any pre-specified large upper limit. However, count models are typically considered to be different from random utility models such as the multinomial logit (MNL) model. In this research, Generalized Extreme Value (GEV) models that are consistent with the Random Utility Maximization (RUM) framework and that subsume standard count models including Poisson, Geometric, Negative Binomial, Binomial, and Logarithmic models as special cases were developed. The ability of the Maximum Likelihood (ML) inference approach to retrieve the parameters of the resulting GEV count models was examined using synthetic data. The simulation results indicate that the ML estimation technique performs quite well in terms of recovering the true parameters of the proposed GEV count models. Also, the models developed were used to analyze the monthly telecommuting frequency decisions of workers. Overall, the empirical results demonstrate superior data fit and better predictive performance of the GEV models compared to standard count models.
PI: Rajesh Paleti
Count models are used for analyzing outcomes that can only take non-negative integer values with or without any pre-specified large upper limit. However, count models are typically considered to be different from random utility models such as the multinomial logit (MNL) model. In this research, Generalized Extreme Value (GEV) models that are consistent with the Random Utility Maximization (RUM) framework and that subsume standard count models including Poisson, Geometric, Negative Binomial, Binomial, and Logarithmic models as special cases were developed. The ability of the Maximum Likelihood (ML) inference approach to retrieve the parameters of the resulting GEV count models was examined using synthetic data. The simulation results indicate that the ML estimation technique performs quite well in terms of recovering the true parameters of the proposed GEV count models. Also, the models developed were used to analyze the monthly telecommuting frequency decisions of workers. Overall, the empirical results demonstrate superior data fit and better predictive performance of the GEV models compared to standard count models.
Implicit Choice Set Generation in Discrete Choice Models: Application to Household Auto Ownership Decisions
PI: Rajesh Paleti
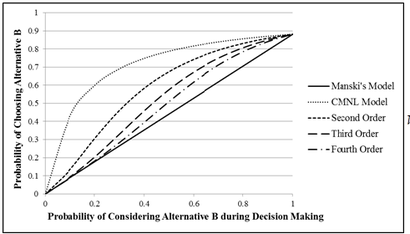
Latent choice set models that account for probabilistic consideration of choice alternatives during decision making have long existed. The Manski model that assumes a two-stage representation of decision making has served as the standard workhorse model for discrete choice modeling with latent choice sets. However, estimation of the Manski model is not always feasible because evaluation of the likelihood function in the Manski model requires enumeration of all possible choice sets leading to explosion for moderate and large choice sets. In this study, we propose a new group of implicit choice set generation models that can approximate the Manski model while retaining linear complexity with respect to the choice set size. We examined the performance of the models proposed in this study using synthetic data. The simulation results indicate that the approximations proposed in this study perform considerably well in terms of replicating the Manski model parameters. We subsequently used these implicit choice set models to understand latent choice set considerations in household auto ownership decisions of resident population in the Southern California region. The empirical results confirm our hypothesis that certain segments of households may only consider a subset of auto ownership levels while making decisions regarding the number of cars to own. The results not only underscore the importance of using latent choice models for modeling household auto ownership decisions but also demonstrate the applicability of the approximations proposed in this study to estimate these latent choice set models.
PI: Rajesh Paleti
Latent choice set models that account for probabilistic consideration of choice alternatives during decision making have long existed. The Manski model that assumes a two-stage representation of decision making has served as the standard workhorse model for discrete choice modeling with latent choice sets. However, estimation of the Manski model is not always feasible because evaluation of the likelihood function in the Manski model requires enumeration of all possible choice sets leading to explosion for moderate and large choice sets. In this study, we propose a new group of implicit choice set generation models that can approximate the Manski model while retaining linear complexity with respect to the choice set size. We examined the performance of the models proposed in this study using synthetic data. The simulation results indicate that the approximations proposed in this study perform considerably well in terms of replicating the Manski model parameters. We subsequently used these implicit choice set models to understand latent choice set considerations in household auto ownership decisions of resident population in the Southern California region. The empirical results confirm our hypothesis that certain segments of households may only consider a subset of auto ownership levels while making decisions regarding the number of cars to own. The results not only underscore the importance of using latent choice models for modeling household auto ownership decisions but also demonstrate the applicability of the approximations proposed in this study to estimate these latent choice set models.




